Build ISO 17025‑Ready Uncertainty BudgetsWithout Spreadsheets or Black Boxes
A browser‑based uncertainty evaluation tool implementing the GUM (JCGM 100:2008), designed to support ISO/IEC 17025 Clause 7.6 with transparent, assessor‑reviewable calculation steps.
Transparent
Every calculation step is explicit and reviewable
GUM-Correct
Strict implementation of JCGM 100:2008
Assessment-Ready
Structured for ISO/IEC 17025 technical review
Why not spreadsheets?
Application Interface
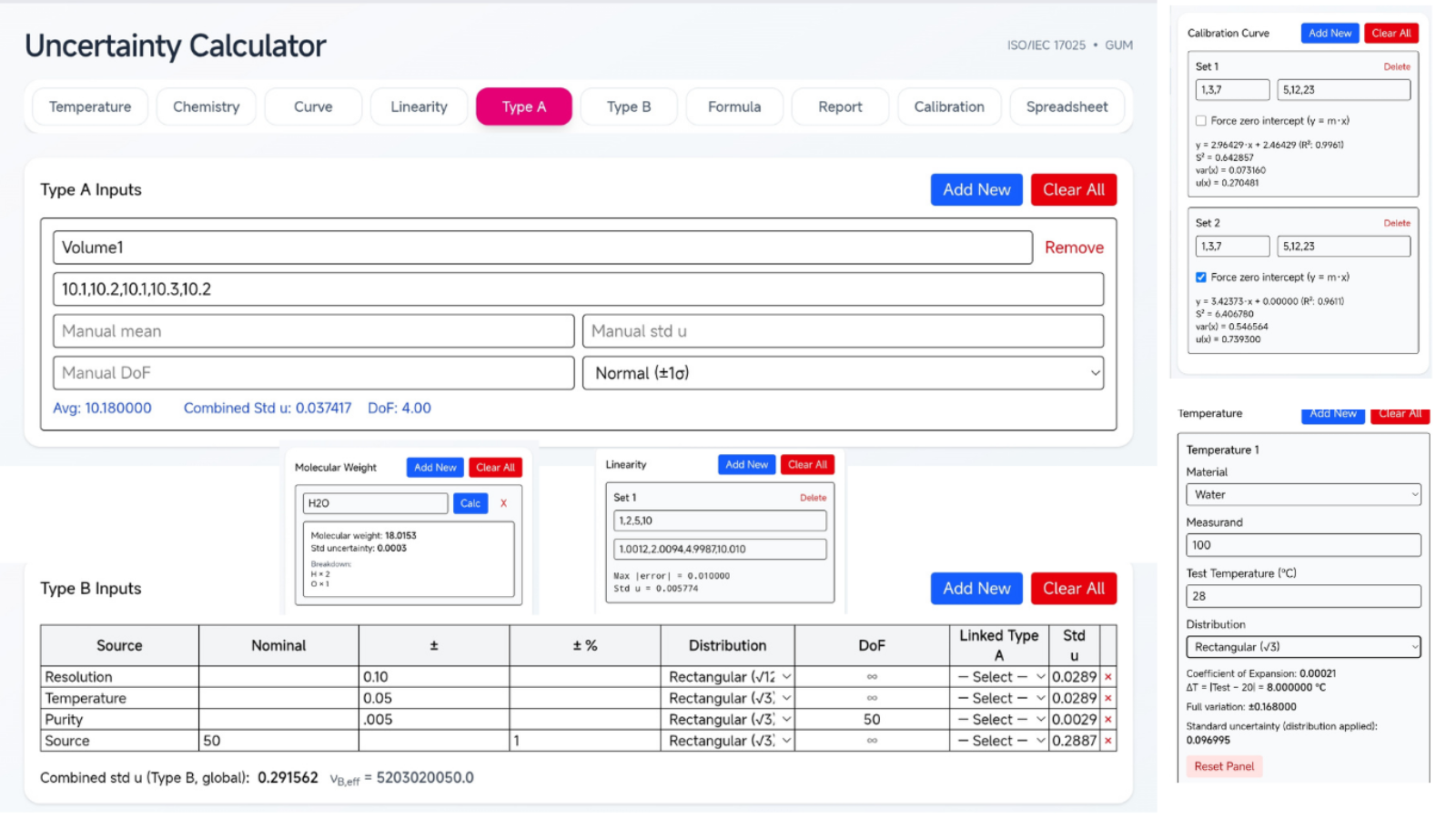
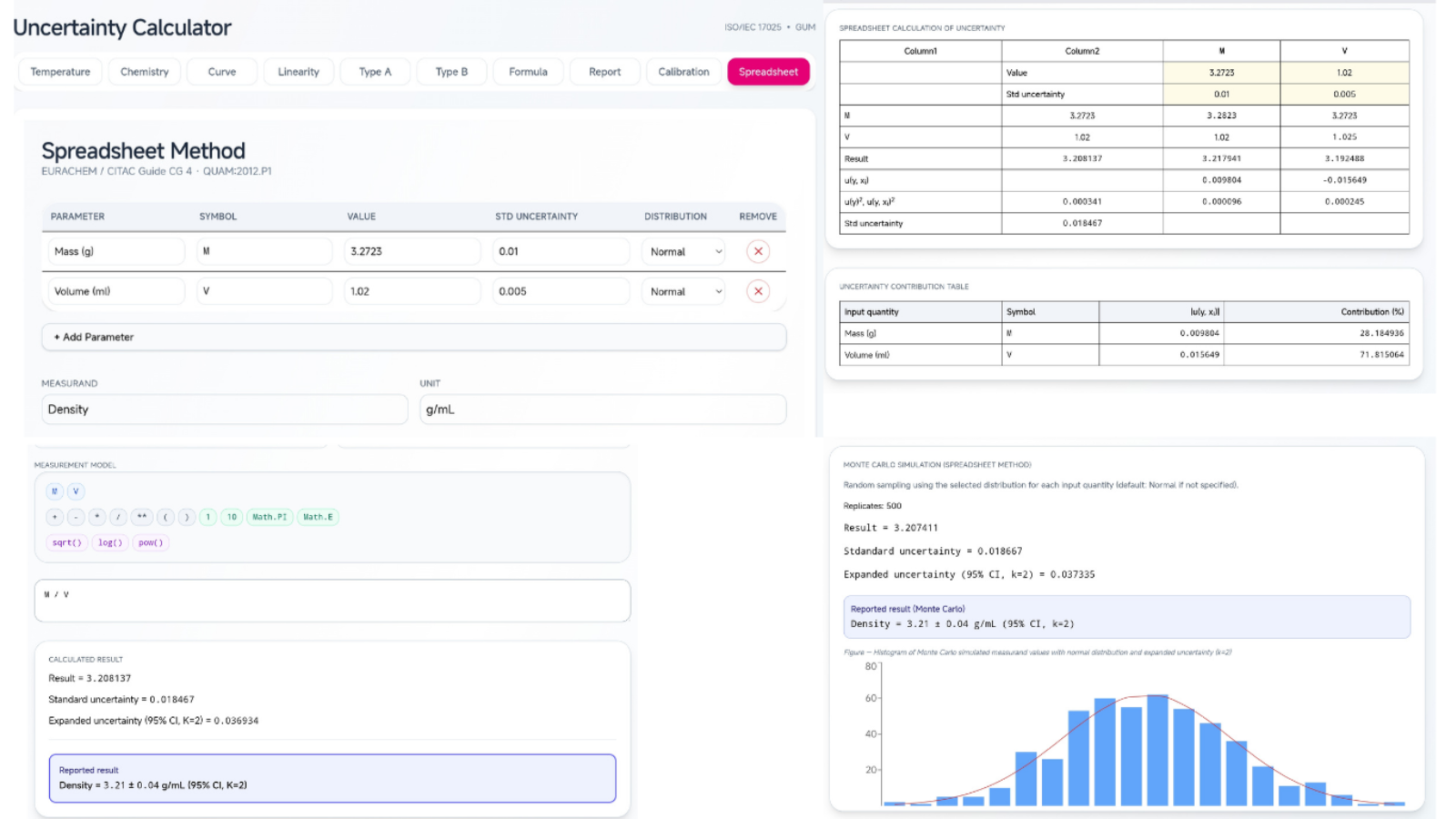
Measurement Uncertainty Methodology
1. Purpose, Scope, and Standards
This methodology describes the principles, assumptions, and calculation procedures implemented in the Uncertainty Calculator for the evaluation of measurement uncertainty. The methodology is written to support laboratories operating under ISO/IEC 17025:2017, with particular reference to Clause 7.6 (evaluation of measurement uncertainty) and Clause 7.8.3 (reporting of results).
The implemented approach follows the Guide to the Expression of Uncertainty in Measurement (GUM, JCGM 100:2008). It is intended to produce technically valid, transparent, and reviewable uncertainty statements suitable for internal verification and external assessment. This methodology supports compliance but does not constitute a claim of accreditation.
2. Measurement Model
Each uncertainty evaluation begins with the explicit definition of a measurement model. The measurand y is defined as a function of one or more input quantitiesx₁, x₂, …, xₙ according to:
y = f(x₁, x₂, …, xₙ)
All input quantities are expressed as estimates with associated standard uncertainties. The validity of the uncertainty evaluation depends on the correctness and applicability of the defined measurement model. Responsibility for defining and justifying the model remains with the laboratory.
3. Type A Uncertainty Evaluation
A Type A evaluation of standard uncertainty is obtained from statistical analysis of repeated observations, in accordance with GUM §§4.2–4.3. This approach is used when repeated measurements of the same measurand are available under appropriate conditions of repeatability or reproducibility.
When the reported result is the arithmetic mean of n observations, the standard uncertainty associated with random effects is calculated as:
uA = s / √n
where s is the experimental standard deviation of the observations. The associated degrees of freedom are equal to n − 1 and are retained for subsequent determination of effective degrees of freedom.
4. Type B Uncertainty Evaluation
A Type B evaluation of standard uncertainty is used when a component of uncertainty is evaluated by means other than statistical analysis of repeated observations, as defined in GUM §4.3. This evaluation is based on scientific judgment using all available information relevant to the possible variability of the input quantity.
Sources of information may include calibration certificates, manufacturer specifications, reference data, previous measurement results, and documented experience. Each source is assessed for validity, relevance, and applicability.
An appropriate probability distribution is selected to model the uncertainty component. For example, when only upper and lower bounds are known and all values are considered equally probable, a rectangular distribution is applied:
uB = a / √3
5. Combination of Uncertainty Components
The combined standard uncertainty is evaluated using the law of propagation of uncertainty in accordance with GUM Clause 5. A first‑order Taylor series expansion of the measurement model is applied.
uc(y) = √( Σ ( cᵢ · u(xᵢ) )² )
The sensitivity coefficients cᵢ are partial derivatives of the measurement function evaluated at the expected values of the input quantities. Unless otherwise justified, input quantities are assumed to be uncorrelated.
6. Degrees of Freedom and Expanded Uncertainty
When uncertainty components are associated with finite degrees of freedom, the effective degrees of freedom of the combined standard uncertainty are estimated using the Welch–Satterthwaite equation, as recommended in GUM Clause 6.
The expanded uncertainty U is obtained by multiplying the combined standard uncertainty by a coverage factor k determined from the Student t‑distribution for the desired level of confidence:
U = k · uc
For sufficiently large effective degrees of freedom, k ≈ 2 may be used to achieve a level of confidence of approximately 95 %.
7. Reporting, Limitations, and Responsibility
Reported measurement results shall include the measured value, the expanded uncertainty, and the applied coverage factor, in accordance with ISO/IEC 17025 Clause 7.8.3. All assumptions and distribution models used in the evaluation shall be documented.
The methodology assumes linear measurement models suitable for first-order uncertainty propagation and independent input quantities unless explicitly stated otherwise. In addition to analytical GUM-based propagation, the calculator implements Monte Carlo methods in accordance with GUM Supplement 1 where applicable.
Final responsibility for the validity, suitability, and reporting of uncertainty results remains with the laboratory.
Appendix A — Code‑to‑Methodology Traceability
This appendix establishes traceability between the documented measurement uncertainty methodology and its implementation within the application codebase. The purpose of this mapping is to demonstrate transparency and assessor reviewability of how methodological elements are exposed to users through the application interface. Numerical execution of calculations is performed by dedicated calculator logic invoked by the application. The application interface layer serves as the controlled entry point for user interaction, presentation, workflow control, and user guidance, and does not perform numerical computation itself.
| Methodology Element | GUM / ISO Reference | Implementation in App.tsx |
|---|---|---|
| Purpose, scope, and standards | ISO/IEC 17025 7.6.1; GUM §2 | Hero section and introductory methodology text rendered in LandingPage component |
| Measurement model definition | GUM §4.1 | Measurement Model accordion explaining y = f(x₁…xₙ) within Methodology section |
| Type A uncertainty evaluation | GUM §4.2 | Type A accordion content; statistical formulae displayed and contextualized in UI |
| Type B uncertainty evaluation | GUM §4.3–4.4 | Type B accordion content describing source data and distribution assumptions |
| Combination of uncertainty components | GUM Clause 5 | Combination formula presented in Methodology; calculation triggered via UI workflow |
| Expanded uncertainty and coverage factor | GUM Clause 6 | Expanded uncertainty explanation and k‑factor guidance rendered in Methodology section |
| Uncertainty budget presentation | GUM Annex H | Budget‑style layout referenced in screenshots and surfaced through application UI |
Appendix B — Software Validation & Verification
This appendix describes the validation and verification activities applied to the Uncertainty Calculator software in support of ISO/IEC 17025:2017 Clauses 7.2 (Selection, verification and validation of methods) and 7.7 (Ensuring the validity of results). The purpose of these activities is to demonstrate that the software performs as intended, implements the documented methodology correctly, and produces technically valid results when used within its defined scope.
| ISO/IEC 17025 Clause | Requirement | Validation / Verification Approach |
|---|---|---|
| 7.2.1 | Selection of appropriate methods | Implementation of GUM (JCGM 100:2008), a recognized international standard; applicability and limitations defined in the Methodology section. |
| 7.2.2 | Verification of methods | Comparison of calculator outputs against independently calculated reference examples, including worked GUM examples and laboratory-approved uncertainty budgets. |
| 7.2.3 | Validation where standard methods are modified | No modification of the GUM methodology is implemented. First-order propagation per GUM Clauses 4–6 is applied. Known limitations are explicitly stated. |
| 7.7.1 | Ensuring the validity of results | User review of inputs, transparent formulas, documented assumptions, and comparison with historical or alternative calculations where appropriate. |
| 7.7.2 | Monitoring of results | Support for repeat evaluations and reproducibility checks by allowing identical input sets to be re-evaluated and compared. |
Validation and verification activities are performed within the scope defined by the laboratory. The software provides computational support and transparency; final responsibility for method selection, validation, and acceptance of results remains with the laboratory in accordance with ISO/IEC 17025.
Appendix C — Risk-Based Software Limitation Statement
In accordance with ISO/IEC 17025:2017 risk-based thinking (Clauses 7.2 and 7.7), the Uncertainty Calculator is designed to mitigate risks associated with incorrect or non-transparent uncertainty evaluations while acknowledging defined limitations.
The software implements first-order uncertainty propagation in accordance with the Guide to the Expression of Uncertainty in Measurement (GUM, JCGM 100:2008) and supports Monte Carlo simulation as described in GUM Supplement 1. First-order methods are suitable for linear or approximately linear measurement models with independent input quantities, while the Monte Carlo method may be applied to linear and non-linear models, including cases involving non-normal distributions or correlated inputs, provided that input assumptions are appropriately defined by the laboratory.
Risks associated with inappropriate model selection, incorrect input data, or misuse of results are mitigated through explicit presentation of formulas, assumptions, probability distributions, and coverage factors. The user is required to review and accept all inputs prior to result generation.
Residual risk remains where the calculator is applied outside its defined scope. In such cases, ISO/IEC 17025 requires that the laboratory perform additional validation or select alternative evaluation methods. Final responsibility for assessing suitability and accepting results remains with the laboratory.
Appendix D — Assessor FAQ
Q: Does this software replace the laboratory’s responsibility for uncertainty evaluation?
A: No. The software provides computational support and transparency. ISO/IEC 17025 places full responsibility for method selection, validation, and result acceptance on the laboratory.
Q: Which uncertainty methodology is implemented?
A: The calculator implements the Guide to the Expression of Uncertainty in Measurement (GUM, JCGM 100:2008), including Type A and Type B evaluations, first-order propagation, and expanded uncertainty.
Q: Are Monte Carlo methods supported?
A: Yes. Support for Monte Carlo methods as specified in GUM Supplement 1 is provided. This functionality is documented and should be taken into account when assessing suitability.
Q: How is software correctness verified?
A: Verification is performed by comparison with independently calculated reference examples, worked GUM examples, and laboratory-approved uncertainty budgets, as described in Appendix B.
Q: How are changes to the software controlled?
A: Software changes are subject to version control and review. Laboratories are expected to verify continued suitability following updates in accordance with ISO/IEC 17025 Clause 7.11.
Prepare uncertainty budgets with confidence
Evaluate measurement uncertainty the GUM-correct way and support ISO/IEC 17025 technical review without spreadsheet risk.